To the nearest pound, the weight of the astronaut 100 miles above earth is 196 pounds
How to get the weight
We have to solve for the weight using this proportion
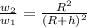
such that w₁ = weight of the astronaut obn earth surface = 206
w₂ = weight above earth
R = 4000
h = 100
We have to put the values on the formula
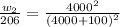
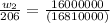
when we solve the equation above we have
206 * 16000000 = w₂ * 16810000
3296000000 / 16810000 = w₂
w₂ = 196.07
To the nearest pound, the weight of the astronaut 100 miles above earth is 196 pounds