Question

The function f(x) = –x2 + 24x – 80 models the hourly profit, in dollars, a shop makes for selling coffee, where x is the number of cups of coffee sold, and f(x) is the amount of profit.

Part A: Determine the vertex. What does this calculation mean in the context of the problem? (5 points)
Part B: Determine the x-intercepts. What do these values mean in the context of the problem? (5 points)
I have the vertex and the x-intercepts but i need to know what they mean in the context of the problem.

Answer 1

The vertex is the maximum y-value of the function. In terms of context, it is when the most amount of profit is obtained during the hour.

The x-intercepts are when the number when the amount of profit selling coffee is equal to 0.

Hope this helps!!

Answer 2

Part A : The vertex is (12,60) . this tells us that the maximum amount of profit i.e. 60 is obtained by selling 12 cups of coffee.

Part B: x-intercept are 4 and 20

x intercept means the number of cups of coffee sold when the amount of profit is 0.

Explanation:

Given :
`f(x)=-x^2+24x-80`

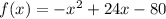
The function models the hourly profit, in dollars, a shop makes for selling coffee, where x is the number of cups of coffee sold, and f(x) is the amount of profit.

Solution:

Standard equation:
`y-k=4p(x-h)^2`

where (h,k) is the vertex

Convert the given equation in standard form.

`y= -x^2+24x-80`

`y= -(x^2-24x+80)`

`y= -(x^2-24x +12^2-12^2+80)`

`y= -((x-12)^2-144+80)`

`y= -((x-12)^2-60)`

`y= -(x-12)^2+60`

`y-60= -(x-12)^2`

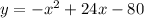
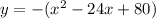
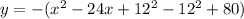
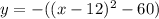
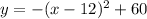
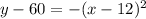
Thus the vertex is (12,60)

Part A : The vertex is (12,60) . this tells us that the maximum amount of profit i.e. 60 is obtained by selling 12 cups of coffee.

Part B: x-intercept

To Find x intercept substitute y =0

`0= -x^2+24x-80`

`x^2-24x+80=0`

`x^2-20x-4x+80=0`

`x(x-20)-4(x-20)=0`

`(x-20)(x-4)=0`

`x=4,20`

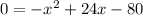
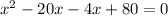
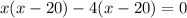
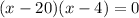
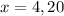
So, x-intercept are 4 and 20

x intercept means the number of cups of coffee sold when the amount of profit is 0.