Question

Identify the oblique asymptotes of f(x)=2x^2-5x+2 over x-3

Answer 1

`\bf \cfrac{2x^2-5x+2}{x-3}\qquad \begin{array}r 3&2&-5&2\\ &&6&3\\ --&--&--&--\\ &2&1&5 \end{array} \\\\\\ quotient=\underline{2x+1}\qquad remainder=5 \\\\\\ \textit{thus oblique asymptote is }y=\underline{2x+1}`

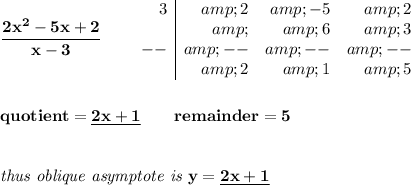
oblique/slant asymptotes occur when the degree of the numerator is exactly 1 greater than that of the denominator

and the oblique asymptote occurs at the quotient of the rational expression, notice, since the denominator is just x - 3, doing a quick synthetic division will do to get the quotient.