Question

Part A : Identify the error Javier made whendetermining the zeros.Part B : Determine the correct zeros of the function.

Answer 1

To determine the zeros of the quadratic function:

`f(x)=x^2-14x+19`

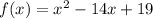
We can use the Quadratic formula given below:

`\begin{gathered} x=\frac{-b\pm\text{ }\sqrt[]{(b^2-4ac)}}{2a} \\ \text{Where a=1; b=-14; c=19} \end{gathered}`

Substituting the above values into the quadratic formula above, we get

`\begin{gathered} x=\frac{-(-14)\pm\text{ }\sqrt[]{(-14)^2-4(1)(19)}}{2*1} \\ \\ x=\frac{14\pm\text{ }\sqrt[]{196-76}}{2} \\ \\ x=\frac{14\pm\sqrt[]{120}}{2}\text{ } \\ \\ x=\frac{14\pm\sqrt[]{4*30}}{2} \\ \\ x=\frac{14\pm2\text{ }\sqrt[]{30}}{2} \\ \\ x=\frac{2(7\pm\text{ }\sqrt[]{30})}{2} \\ \\ x=\text{ 7}\pm\text{ }\sqrt[]{30} \end{gathered}`

Clearly, Javier's error is that he did not factor out the 2 attached to the square root before he divided by 2 to arrive at his answer.

Hence, the correct answer is

`x=7\pm\text{ }\sqrt[]{30}\text{ }\Rightarrow\text{ x=7}+\text{ }\sqrt[]{30}\text{ or x =7 - }\sqrt[]{30}`