Question

In her wallet, Ms. Thompson has one-dollar, five-dollar, and ten-dollar bills, totally $171. She has the same number of five-dollar bills as one-dollar and ten-dollar bills put together. If she has 30 bills in all, how many bills of each denomination does she have?

Answer 1

Let's check. 6 one-dollars = $6 15 five-dollars = $75 9 ten-dollars = $90 Add them all up to get $171, so that is correct. Add the number of one-dollar bills and the number of ten-dollar bills together. 6 + 9 = 15, which is the number of five-dollar bills, so that is correct as well. Add all the numbers of bills together, 6 + 9 + 15 = 15 + 15 = 30, so that is correct

Answer 2

She has 6 one dollar, 15 five dollar and 9 ten dollar of bills in her wallet.

Explanation:

Consider the provided information.

Ms. Thompson has one-dollar, five-dollar, and ten-dollar bills, totally $171.

Let x represents the number of one dollar bills.

y represents the number of five dollar bills.

z represents the number of ten dollar bills.

She had one-dollar, five-dollar, and ten-dollar bills, totally $171.

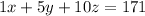`1x + 5y + 10z =171`......(1)

She has the same number of five-dollar bills as one-dollar and ten-dollar bills put together.

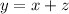`y=x+z`.....(2)

She has 30 bills in all.

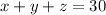`x+y+z=30` ......(3)

Substitute the value of x+z in equation 3.

`y+y=30`

`y=15`

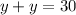
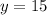
Substitute the value of y in equation 2

`15=x+z`

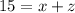
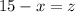`15-x=z` ......(4)

Substitute the value of y and z in equation 1.

`1x + 5(15) + 10(15-x) =171`

`x + 75 + 150-10x=171`

`54=9x`

`x=6`

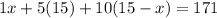
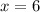
Now substitute the value of x in equation 4.

`15-6=z`

`9=z`

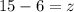
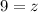
Hence, she has 6 one dollar, 15 five dollar and 9 ten dollar of bills in her wallet.