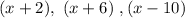2 Answers

Stdcall · Answer 1 · 2018-06-21T10:46:09+0000

Since

, it follows by the polynomial remainder theorem that
f(x)

is perfectly divisible by
x+2

. Dividing, we have

(x^3-2x^2-68x-120)/(x+2)=x^2-4x-60

and factoring further, we have

f(x)=(x+2)(x^2-4x-60)=(x+2)(x+6)(x-10)

Guranjan Singh · Answer 2 · 2018-06-27T17:47:39+0000

Answer:

All the factors of the function f(x) are:

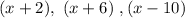
$(x+2),\ (x+6)\ ,(x-10)$

i.e.

$f(x)=x^3-2x^2-68x-120=(x+2)\cdot (x+6)\cdot (x-10)$

We are given a cubic function f(x) in terms of variable x as follows;

f(x)=x^3-2x^2-68x-120

Also, we are given that:

f(-2)=0

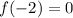
This means that -2 is a zero of the function f(x)

Hence, f(x) could be written in the form of:

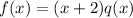
f(x)=(x+2)q(x)

where q(x) is a two degree polynomial.

i.e. we get:

$q(x)=(f(x))/(x+2)\\\\i.e.\\\\q(x)=(x^3-2x^2-68x-120)/(x+2)\\\\i.e.\\\\q(x)=x^2-4x-60$

We can factorize q(x) further by using the method of splitting the middle term as follows:

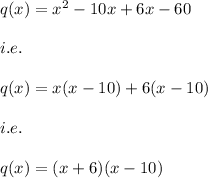
$q(x)=x^2-10x+6x-60\\\\i.e.\\\\q(x)=x(x-10)+6(x-10)\\\\i.e.\\\\q(x)=(x+6)(x-10)$

i.e. The factors of f(x) are:

$(x+2),\ (x+6)\ ,(x-10)$