Question

Find the value of x and the value of y. A. x = 15, y = 10 B. x = 20, y = 50 C. x = 50, y = 10 D. x = 50, y = 20

Answer 1

The answer is c. X=50 because 5x-100+(x-20)=180. Y=10 when you solve for 30+y+140=180

Answer 2

Option C is correct that is x=50 and y=10.

Explanation:

The angles given are vertically opposite angles:

Due to that property we will have

`(3y)^(\circ)=(x-20)^(\circ)`

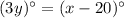
And
`(y+140)^(\circ)=(5x-100)^(\circ)`

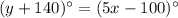
we will rearrange the above equations as:

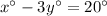`x^(\circ)-3y^(\circ)=20^(\circ)` (1)

And
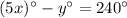`(5x)^(\circ)-y^(\circ)=240^(\circ)` (2)

Now, we will solve the equations by elimination method:

Multiply equation (2) by 3 we get:

`x-3y=20`

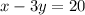
And
`15x-3y=720`

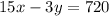
Add above two equations we get:

14x=700

x=50

Now, put x=50 in x-3y=20 we get:

50-3y=20

y=10

Therefore, Option C is correct that is x=50 and y=10.