Question

Which shows the graph of the solution set of 3y – 2x > –18?

Answer 1

Were are the graphs?

Answer 2

`3y-2x>-18`

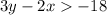
Explanation:

We are given with a linear equation
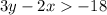`3y-2x> -18` . We have to draw this inequality.

In order to draw this inequality , we have to first draw the graph of

`3y-2x= -18`

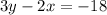
Let us do it , by converting the equation into intercept form, and find the x and y intercepts.

Divide both side, each term by -18 , we get

`(3y)/(-18)-(2x)/(-18)= (-18)/(-18)`

`(y)/(-6)-(x)/(-9)= 1`

`(y)/(-6)+(x)/(9)= 1`

`(x)/(9)+(y)/(-6)= 1`

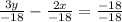
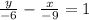
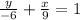
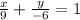
Hence our x intercept = 9

y intercept = -6

Hence the line passes through the coordinates (9,0) and (0,-6). We now plot them on graph and draw our line.

Now we have to check which region to shade.

Our inequality is given as
`3y-2x>-18`

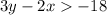
Let us see whether (0,0) satisfies this inequality. For that we need to substitute them in our equation.

`3(0)-2(0)>-18`

`0-0>-18`

`0>-18`

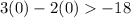
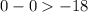
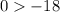
Which is true .

Hence , we shade the region which is containing (0,0) . Also our line need to be broken as it is containing > sign in it.