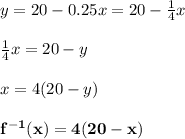The inverse of a function is obtained by making x the subject of the formular of the function.
Given the function
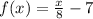
the inverse of the function is obtained as follows:

Given the function
[tex[f(x)=x+7[/tex]
the inverse of the function is obtained as follows:
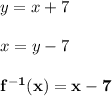
Given the function

the inverse of the function is obtained as follows:

Given the function
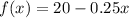
the inverse of the function is obtained as follows: