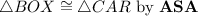Question

Hey guys! I have a problem that I can't solve. Help please! 14 points! There are 2 screenshots: 1 as for the triangle, and 1 for the rules.

Answer 1

ASA/AAS

Skills needed: Triangle Geometry

Explanation:

1) When looking at Triangles, there are 5 ways to determine Congruence.

---> SSS - When all 3 sides of one triangle are congruent to the other. (The tick marks are used to signify the congruent sides - The sides with 1 tick are congruent to each other, the sides with 2 ticks are congruent to each other, and so on).

---> AAA - When all 3 angles of one triangle are congruent to the other. Again, tick marks are used to signify the congruent angles.

---> SAS - When 2 sides of a triangle are congruent, and the angle in between those two sides of the first triangle is congruent to the second triangle.

---> ASA - When two angles and the side in-between the two angles of one triangle are congruent to the other triangle.

---> AAS - When two angles and one of the two sides not in-between the two angles of the first triangle are congruent to the other triangle.

----------------------------------------------------------------------------------------------------------

As mentioned before, ticks are almost always used to display congruence of sides and angles.

The congruence sign is
`\cong`

----------------------------------------------------------------------------------------------------------

2) In this problem,
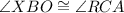`\angle XBO \cong \angle RCA`, meaning the angle denoted by XBO (B is the vertex, and X and O are the endpoints) is congruent to the angle denoted by RCA (C is the vertex, R and A are the endpoints)

---> Also,
`\angle XOB \cong\angle RAC` (Angle XOB is congruent to Angle RAC)

2 angles from the first triangle (
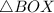`\triangle BOX`) are found to be congruent in the 2nd triangle (
`\triangleCAR`
`\triangle CAR`)

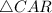---------> ALSO:

-
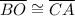`\overline{BO} \cong \overline{CA}` ---> One side from
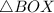`\triangle BOX` is congruent to
`\overline{CA}`, which is from the other triangle.

NOTE: This side is also in-between THE TWO ANGLES STATED BEFORE. This means that we have:

ASA ---> Since this has the side in-between the two angles.

ASA is the answer!

`\triangle BOX \cong \triangle CAR \text{ by } \textbf{ASA}`