Question

f(x) = 7x g(x) = 7x + 6 Which statement about f(x) and its translation, g(x), is true? The domain of g(x) is x , and the domain of f(x) is x . The domain of g(x) is y , and the domain of f(x) is y . The asymptote of g(x) is the asymptote of f(x) shifted six units down. The asymptote of g(x) is the asymptote of f(x) shifted six units up.

Answer 1

the asymptote of g(x) is the aymptote of f(x) shifted six units up

Answer 2

The correct option is 4. The asymptote of g(x) is the asymptote of f(x) shifted six units up.

Explanation:

The given functions are

`f(x)=7x`

`g(x)=7x+6`

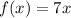
Both are linear function and the domain of a linear function is all real real numbers.

Domain of f(x) = x∈R

Domain of g(x) = x

Therefore option 1 and 2 are incorrect.

The linear asymptote of a linear function
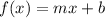`f(x)=mx+b` is

`y=mx+b+\delta x`

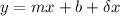
Where, δx is infinitely small number, but not quite equal to 0.

The asymptote of f(x) is

`y=7x+\delta x`

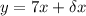
The asymptote of g(x) is

`y=7x+6+\delta x`

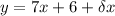
It means the asymptote of f(x) shifts six units up to get the asymptote of g(x).

Therefore option 4 is correct. The asymptote of g(x) is the asymptote of f(x) shifted six units up.