Question

How can you determine which quadrant an equation falls in?

For the equation 2sec²θ - tanθ - 3 = 0
The answers of θ falls in quadrant 2 and 4.
My understanding is that this equation is positive therefore it will fall under quadrant 1 and 3.

Answer 1

`\bf 2sec^2(\theta )-tan(\theta )-3=0 \\\\\\ 2[1+tan^2(\theta )]-tan(\theta )-3=0\implies 2+2tan^2(\theta )-tan(\theta )-3=0 \\\\\\ 2tan^2(\theta )-tan(\theta )-1=0\implies [2tan(\theta )+1][tan(\theta )-1]=0\\\\ -------------------------------\\\\`


`\bf 2tan(\theta )+1=0\implies 2tan(\theta )=-1\implies tan(\theta )=-\cfrac{1}{2} \\\\\\ \measuredangle \theta \approx \begin{cases} 5.82\ radians\\ 2.68\ radians \end{cases}\qquad \begin{array}{llll} \textit{the tangent is negative}\\ \textit{tha means the II and IV quadrants} \end{array}\\\\ -------------------------------\\\\`


`\bf tan(\theta )-1=0\implies tan(\theta )=1\implies \measuredangle \theta = \begin{cases} (\pi )/(4)\\ (7\pi )/(4) \end{cases} \\\\\\ \textit{the tangent is positive}\\ \textit{that means the I and III quadrants}`


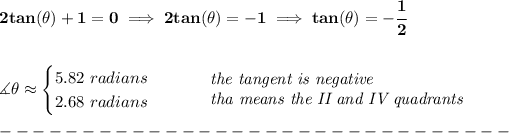
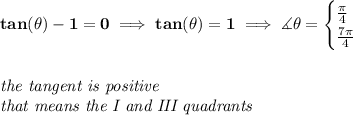
bear in mind that tangent is sine/cosine or y/x

for the tangent to be negative, the signs of "y" and "x" must differ, and that happens only on the II and IV quadrants

and for the tangent to be positive, the signs must be same, and that's only on I and III quadrants.