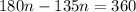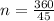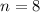Question

An interior angle of a regular polygon has a measure of 135°. What type of polygon is it?

Answer 1

So basically the regular polygon interior angles don't really have an efficient strategy to figure out, there is a formula but it would be better just to memorize it.
Kind of chart below:

Shape Number of Sides Total Interior Angle Single Interior Angle

Triangle 3 sides 180 degrees 60 degrees
Quadrilateral 4 sides 360 degrees 90 degrees
Pentagon 5 sides 540 degrees 108 degrees
Hexagon 6 sides 720 degrees 120 degrees
Heptagon 7 sides 900 degrees 129 ish degrees
Octagon 8 sides 1080 degrees 135 degrees

So it is an octagon.

Answer 2

ANSWER


`\boxed {Octagon}`

Step-by-step explanation


The interior angle of a regular polygon with n sides can be found using the formula,


`((n -2)180 )/(n)`

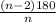
It was given that, the interior angle is 135°.



This implies that,



`((n -2)180 )/(n) = 135`


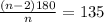
We cross multiply to obtain,



`(n - 2)180 = 135n`


We expand to obtain;



`180 n - 360 = 135n`


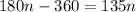
Group like terms to get,


`180n - 135n = 360`



`45n = 360`



`n = (360)/(45)`


`n = 8`