Question

Assume that there is a 5​% rate of disk drive failure in a year. a. If all your computer data is stored on a hard disk drive with a copy stored on a second hard disk​ drive, what is the probability that during a​ year, you can avoid catastrophe with at least one working​ drive? b. If copies of all your computer data are stored on three three independent hard disk​ drives, what is the probability that during a​ year, you can avoid catastrophe with at least one working​ drive?

Answer 1

To calculate the probability that during a year you can avoid catastrophe with at least one working drive, subtract the probability of both drives failing from 1. For two drives, the probability is 0.9975, and for three drives, the probability is 0.999875.

Step-by-step explanation:

To calculate the probability that during a year you can avoid catastrophe with at least one working drive, we can consider the complementary event - the probability that both drives fail. Let's calculate:

a. Probability that at least one drive is working = 1 - Probability that both drives fail

= 1 - (Probability of drive 1 failure * Probability of drive 2 failure)

= 1 - (0.05 * 0.05)

= 1 - 0.0025

= 0.9975

b. Similarly, for three independent drives:

Probability that at least one drive is working = 1 - Probability that all drives fail

= 1 - (Probability of drive 1 failure * Probability of drive 2 failure * Probability of drive 3 failure)

= 1 - (0.05 * 0.05 * 0.05)

= 1 - 0.000125

= 0.999875

Answer 2

The probability that during a​ year, you can avoid catastrophe with at least one working​ drive is 0.9975

The probability that during a​ year, you can avoid catastrophe with at least one working​ drive is 0.999875

Step-by-step explanation:

There is a 5​% rate of disk drive failure in a year

So, probability of failure q = 0.05

Since the sum of probabilities = 1

So, probability of success p= 1-0.05

=0.95

Part a : all your computer data is stored on a hard disk drive with a copy stored on a second hard disk​ drive

So, n =2

We are required to find what is the probability that during a​ year, you can avoid catastrophe with at least one working​ drive

So, he probability that during a​ year, you can avoid catastrophe with at least one working​ drive :

`1-(^2C_0 * p^0* q^2)`

`1-((2!)/(0!(2-0)!)* (0.95)^0*(0.05)^2)`

`1-(1*0.0025)`

`0.9975`

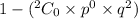
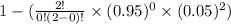
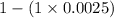
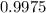
Hence the probability that during a​ year, you can avoid catastrophe with at least one working​ drive is 0.9975

Part b : If copies of all your computer data are stored on three three independent hard disk​ drives, what is the probability that during a​ year, you can avoid catastrophe with at least one working​ drive?

Since there are 3 copies so, n =3

So, the probability that during a​ year, you can avoid catastrophe with at least one working​ drive:

`1-(^3C_0 * p^0* q^2)`

`1-((3!)/(0!(3-0)!) * (0.95)^0*(0.05)^3)`

`1-(1*0.000125)`

`0.999875`

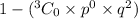
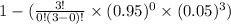
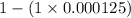
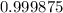
Hence the probability that during a​ year, you can avoid catastrophe with at least one working​ drive is 0.999875