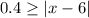Question

he ideal width of a safety belt strap for a certain automobile is 6 cm. An actual width can vary by at most 0.4 cm. Write an absolute value inequality for the range of acceptable widths. Picture of possible answers included.

Answer 1

Answer:
`0.4\geq | x-6|`

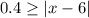
Explanation:

Here the ideal width of a safety belt strap for a certain automobile = 6 cm

And, according to the question,

It can be only vary by at most 0.4 cm.

Thus, the maximum possible width = 6 + 0.4 = 6.4 cm

And the minimum possible width = 6 - 0.4 = 5.6 cm

Let x represents the width of the belt strap after a certain variation,

Then we can write,

`5.6\leq x\leq 6.4`

By subtracting 6 from all sides of the inequality,

`5.6 - 6\leq x\leq 6.4 - 6`

⇒
`- 0.4\leq x-6\leq 0.4`

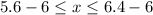
If
`- 0.4\leq x-6`

⇒
`0.4\geq -(x-6)`

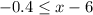
But,
`0.4\geq x-6`

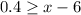
On combining the inequalities,

we get,
`0.4\geq |x-6|`

Answer 2

1. The width of the safety belt is 6 cm, but it can vary by at most 0.4 cm

this means that the width can be at most: 6+0.4= 6.4 (cm)

and at least 6-0.4=5.6 (cm)

so the width x, is represented by the inequality


`5.6 \leq x \leq 6.4`


`6-0.4 \leq x \leq 6+0.4`

subtract 6 from all sides:


`-0.4 \leq x-6 \leq 0.4`

from the rule :
`|A(x)| \leq c` is equivalent to


`-c \leq A(x) \leq c` we have:


`|x-6| \leq 0.4`