Question

The table shows a company’s profit based on the number of pounds of food produced.

Using the quadratic regression model, which is the best  estimate of the profit when 350 pounds of food are produced?




A). 5,150
B). 5,300
C). 10,150
D). 11,000

Answer 1

The answer is B 5,300

Answer 2

B) 5,300

Explanation:

Let x represents the pounds of food produced and y represents the profit in dollars,

Thus, the table that shows the given situation would be,

x 100 250 500 650 800

y -11000 0 10300 11500 9075

Since, the equation of a quadratic equation is,

`y=A+Bx+Cx^2`

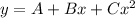
Where,

`A=\overline{y}-B\overline{x}-C(\overline{x})^2`

`B=(S_(xy) S_(x^2x^2)-S_(x^2y)S_(xx^2))/(S_(xx).S_(x^2x^2)-(S_(xx^2))^2)`

`C=(S_(x^2y).S_(xx)-S_(xy)S_(xx^2))/(S_(xx)S_(x^2x^2)-(S_(xx))^2)`

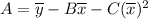
Also,

`S_(xx)=\frac{\sum(x_i-\bar{x})^2}{n}`

`S{xy}=\frac{(x_i-\bar{x})(y_i-\bar{y})}{n}`

`S_(xx^2)=\frac{\sum(x_i-\bra{x})(x_i^2-\bar{x^2})}{n}`

`S_(x^2x^2)=\frac{\sum(x_i-\bar{x^2})^2}{n}`

`S_(x^2y)=\frac{\sum (x_i^2-\bar{x^2})(y_i-\bar{y})}{n}`

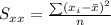
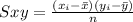
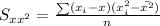
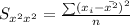
By substituting the values,

We get,

A ≈ -20420.96

B ≈ 102.24

C ≈ -0.082

Hence, the quadratic equation that shows the given situation is,

`y=-20420.96+102.24x-0.082x^2`

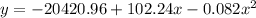
For x = 350 pounds,

`y=-20420.96+102.24(350)-0.082(350)^2`

`=5318.04`

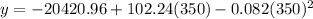
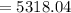
Which is nearby 5300,

Hence, option B is correct.