Question

A rocket is launched from atop a 99-foot cliff with an initial velocity of 122 ft/s.

a. Substitute the values into the vertical motion formula h = -16t^2 + vt + c. Let h = 0.
 b. Use the quadratic formula find out how long the rocket will take to hit the ground after it is launched. Round to the nearest tenth of a second.

Answer 1

8.4 seconds

Explanation:

For (a) we have h=0 and t=0

when we substitute the values we get

`0=-16\cdot 0^2+122\cdot 0+c`

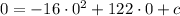
Which will give the value c=0

Now, to find how long the rocket will take to hit the ground after it is launched

we get
`0=-16\cdot t^2+122\cdot t+99`

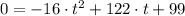
We will solve the above quadratic equation for t we get:

`16t^2-122t-99=0`

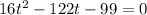
We have formula to solve the quadratic equation:

Here, a=16, b=-122 and c=-99

On substituting the values in the formula we get:

`D=(-122)^2-4(16)(-99)=21220`

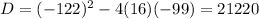
Now, we will substitute D in the formula to get final value of t

`t=(-(-122)\pm√(145.67))/(2(16))`

`t=(122\pm√(145.67))/(32)`

`t=8.36,-0.73`

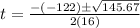
We will neglect the negative time

Hence, 8.36 seconds or approximately 8.4 seconds