Question

An engineer on the ground is looking at the top of a building. The angle of elevation to the top of the building is 22°. The engineer knows the building is 450 ft tall. What is the distance from the engineer to the base of the building to the nearest whole foot?

1,114 ft

1,201 ft

1,818 ft

990 ft

Answer 1

Let the distance of the engineer from the base of the building be x, then
tan 22 = 450/x
x = 450/tan 22 = 450/0.4040 = 1,113.79

Therefore, the distance of the engineer from the base of the building to the nearest foot is 1,114 feet.

Answer 2

Distance, x = 1114 ft

Explanation:

It is given that,

The angle of elevation to the top of the building,
`\theta=22^0`

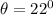
Height of the building, h = 450 ft

We have to find the distance from the engineer to the base of the building i.e. x

In triangle ABC, using trigonometric equations as :

`tan(22)=(AB)/(BC)`

`tan(22)=(450)/(x)`

`x=(450)/(tan(22))`

`x=1113.7\ ft`

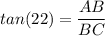
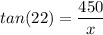
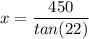
or

x = 1114 ft

So, the distance from the engineer to the base of the building is option (A) i.e. 1114 ft