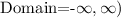We have the following relation:
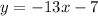
And we have to determine if that relationship between both variables is a function.
1. To achieve that, we need to remember that:
• A function is a relation in which there is exactly one output for each input.
,
• The set of all the inputs for a function is the domain of the function.
,
• The set of all the outputs for a function represents the range of the function
,
• If we have to define a function, we have to describe the rule of that function.
2. We can see that the relation above is of the form:

Where
• m is the slope of the line. In this case, m = -13, which is a negative slope.
,
• b is the y-intercept of the line, and it is the point where the line passes through the y-axis, and when x = 0. In this case, b = -7.
Then the rule of the function is given by y = -13x - 7.
3. Therefore, this is a linear function, and in this case, we have that the rule assigns exactly one y-value to each distinct x-value in the domain. Likewise, the domain in this kind of function is the set of all the real numbers, and we can write it in interval notation as follows:
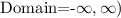
Hence, in summary, we can say that:
A. Yes, the equation y =- 13x- 7 assigns exactly one y-value to each distinct x-value in the domain.
The domain is (in interval notation) is: