Question

Which of the following are equivalent to the function y = 4cos x - 2? a. y= 4sin(x-pi/2)-2 b. y=4sin(x+pi/2) - 2 c. y=4cos(-x)-2 d. y=-4cos x +2.

Answer 1

To answer this question, we must know some identities:
1. cos(x) is an even function, so cos(x)=cos(-x) [this makes choice (c) true]
2. sin(x) and cos(x) are the same periodic functions with a phase-shift of pi/2, so that sin(x+pi/2)=cos(x) [this makes choice (b) true]
3. also, sin(x) is symmetrical about pi/2, and cos(x) is symmetrical about x=0. This means that sin(x)=cos(pi/2-x) [ this case is not present in the choices ]

Answer 2

Option b and c is correct.

Explanation:

Given : Function
`y=4\cos x-2`

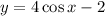
To find : Which of the following are equivalent to the function?

Solution :

The function given is
`y=4\cos x-2`

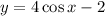
We know that,

`\cos(-x)=\cos(x)`

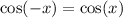
and
`\sin((\pi)/(2)+x)=\cos(x)`

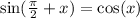
Applying these in the given function,

Using,
`\cos(-x)=\cos(x)`

`y=4\cos (-x)-2`

`y=4\cos (x)-2`

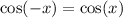
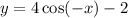
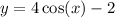
So option c is equivalent.

Using,
`\sin((\pi)/(2)+x)=\cos(x)`

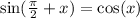
Substitute

`y=4\sin((\pi)/(2)+x)-2`

`y=4\cos (x)-2`

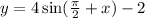
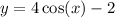
So option b is equivalent.

Therefore, Option b and c is correct.