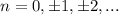Usually one will differentiate the function to find the minimum/maximum point, but in this case differentiating yields:
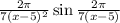
which contains multiple solution if one tries to solve for x when the differentiated form is 0.
I would, though, venture a guess that the minimum value would be (approaching) 5, since the function would be undefined in the vicinity.
If, however, the function is
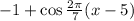
Then differentiating and equating to 0 yields:
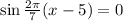
which gives:

or
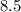
We reject x=5 as it is when it ix the maximum and thus,
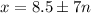
, for