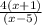1. We are asked to simplify the expression :
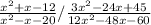
2. First thing we can do is to flip the second expression, so make the division a multiplication, and also factorize 3 in the numerator and 12 in the denominator of the second expression as follows:
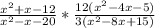
3. Now factorize each of the quadratric expressions using the following rule:
when we want to factorize
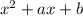
, we look for 2 numbers m and n, whose sum is a, and product is b:
for example: in
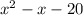
, the 2 numbers we are looking for are clearly -5 and 4, because (-5)+4=-1, (-5)*4=-20, so we write the factorized form (x-5)(x+4)
Now apply the rule to the whole expression:
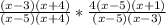
4. Simplify equal terms in the numerator and denominator:
we get:
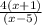
Answer: