Question

A rock on the top of a hill has a gravitational potential energy. If the hill is 10.2 m high, how fast will the rock be rolling when it reaches the bottom - write out that equation and see if anything cancels out.

Answer 1

`\begin{equation*} 14.14\text{ }m\/s \end{equation*}`

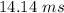
Step-by-step explanation

We want to find the speed of the rock when it reaches the bottom.

The gravitational potential energy of the rock at the top of the hill is equal to the kinetic energy of the rock when it reaches the bottom of the hill. This implies that:

`\begin{gathered} PE_(top)=KE_(bottom) \\ mgh=(1)/(2)mv^2 \end{gathered}`

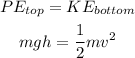
where m = mass of the rock

g = acceleration due to gravity

h = height of the hill

v = speed of the rock at the bottom of the hill

Substituting the given values and solving for v:

`\begin{gathered} gh=(1)/(2)v^2 \\ \Rightarrow v^2=2gh \\ v=√(2gh) \\ v=√(2*9.8*10.2)=√(199.92) \\ v=14.14\text{ }m\/s \end{gathered}`

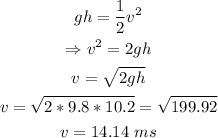
That is the speed of the rock as it reaches the bottom of the hill.