Question

SAT scores are normed so that, in any tear, the mean of the verbal or math test score should be 500 and the standard deviation 100. Assuming this is true, answer the following question. A college decides to liberalize its admission policy. As a first step, the admissions committee decides to exclude only those applicants scoring below the 20th percentile on the verbal SAT. Translate this percentile into a Z score. Then calculate the equivalent SAT verbal test score.

Answer 1

SAT scores have a normal distribution with mean μ=500 and standard deviation σ=100

The admissions committee decided to exclude the applicants scoring below the 20 percentile of the verval SAT.

This means that they'll exclude the lower 20% of the population, you can symbolize this as:

`P(X\leq a)=0.20`

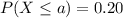
Where "a" represents the SAT score that divides the lowest 20% of the population from the top 80%.

To find this value you have to determine the 20th percentil under the standard normal distribution:

`P(Z\leq b)=0.20`

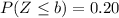
For this look for the value of Z that accumulates 0.20 of distribution. This value of probability is in the left arm of the curve, which means that the Z value "b" will be nagative.

Determine this value using the left entry of the Z-distribution:

b= -0.842 → This value determines the 20th percentile of the distribution.

Derived from the normal distribution is the standard normal distribution. Considering a random variable X with normal distribution, mean μ and variance δ², the variable Z =(X-μ)/δ ~N(0;1) is determined.

So to determine the equivalent SAT score you have to use the formula amd "translate" the determined value of Z to a value of the variable X:

`\begin{gathered} Z=((X-\mu))/(\sigma) \\ b=((a-\mu))/(\sigma) \\ -0.842=(a-500)/(100) \\ -0.842\cdot100=a-500 \\ -84.2=a-500 \\ a=-84.2+500 \\ a=415.8 \end{gathered}`

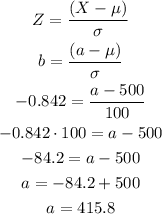
The SAT score that determines the 20th percentile of the scores distribution is 415.8