To solve this, we must set up a
Systems of Equations problem
Let's say
C stands for
Coach seats bought and
S stands for
sleeper cars bought
Here are our equations we have enough information to make.
c + s = 93 115c + 290s = $20,320 Lets solve for Coach seats first
To do that we need a value for s
In the first equation,
s = 93 - cLets plug that in for S in the second equation
115c + 290(93 - c) = $20,320 Distribute and simplify
115c + 26,970 - 290c = $20,320
Combine like terms
-175c + 26,970 = $20,320
-175c = -6650
divide
c =
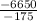 c = 38
c = 38We just found out 38 coach seats were bought.
Plug in 38 for C in this equation ⇒ 115c + 290s = $20,320 to find S
115(38) + 290s = $20,320 Distribute and Simplify
4,370 + 290s = $20,320
290s = $15,950
Divide
S =
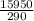 S = 55
S = 55We just completed the problem!
38 Coach seats were bought and 55 Sleeper car seats were bought.