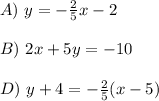Let's rewrite each equation in the Slope-Intercept Form of the Equation of a Line. First, let's start with the main equation:
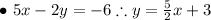
Then, our options are the following:
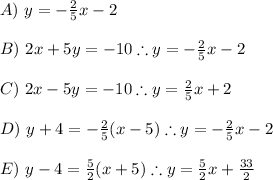
For two perpendicular lines it is true that the product of its slopes is:
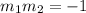
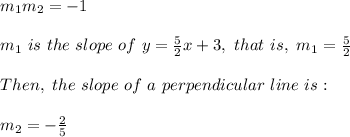
According to this, only A) B) and D) might be the perpendicular lines we are looking for. Notice that these lines are the same. The other condition is that the line must pass through the point (5, -4). By substituting this point in the equation, we have:
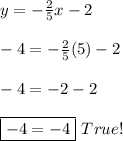
Finally, the right answer are: