To answer this question, we need to obtain two z-scores, one for x = 76, and the other for x = 88. Then, we will need to subtract both cumulative probabilities. We are going to use the cumulative standard normal table to obtain the final values.
Finding the z-score for x = 76
We will use the next formula:

Where
• x = 76 (raw value)
,
• mu = 100 (population mean)
,
• sigma = 12 (standard deviation)
Then, we have:
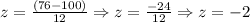
The value is two standard deviations below the population mean. To find the cumulative probability, in this case, we need to consult the cumulative standard normal table:
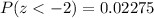
We need to repeat the same procedure for x = 88.
Finding the z-score for x = 88
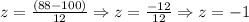
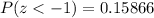
This value is the cumulative probability for a value one standard deviation below the mean.
Percentage of the population that has IQs 76 and 88 (between these two IQs)
Then, the percentage of the population that has these IQs is (the population that is between these two IQs is):
[tex]P(76Therefore,
this percentage is about 13.59% or 13.6% (if we round the value to the nearest tenth).
A graph representing this situation can be seen below: