Recall that the domain of a function is the set of all x values of the function for which the function is defined.
Given that
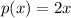
and
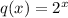
Given that
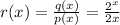
For the function to be undefined, the denominator should be zero
i.e. 2x = 0 which means that x = 0
Thus, the domain of the function is all real values of x except 0.
Therefore, the restriction is x ≠ 0.
Given that
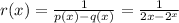
For the function to be undefined, the denominator should be zero
i.e.
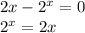
For x = 2,
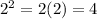
Also, for x = 1
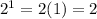
Thus, the domain of the function is all real values of x except 1 and 2.
Therefore, the restriction is x ≠ 1, 2.
Given that
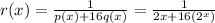
For the function to be undefined, the denominator should be zero
i.e.
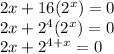
For x = -2,
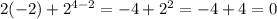
.
Thus, the domain of the function is all real values of x except -2.
Therefore, the restriction is x ≠ -2.
Given that
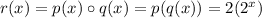
There is no value of x, for which the function is undefined.
Thus, the domain of the function is all real values of x.
Therefore, there is no restrictions to the domain of the function.
Given that
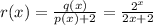
For the function to be undefined, the denominator should be zero
i.e.
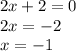
Thus, the domain of the function is all real values of x except -1.
Therefore, the restriction is x ≠ -1.