Question

A rock is thrown upward with a speed of 48 feet per second from the edge of a cliff 400 feet above the ground. What is the speed of the rock when it hits the ground? Use acceleration due to gravity as -32 feet per second squared and approximate your answer to 3 decimal places. (10 points)

Answer 1

Ok here's what I make of this: you're in calculus and you're working with functions and their first derivatives, which are the position function and the velocity function, respectively. You need to figure out what the functions are so you can solve the problem. But the acceleration due to gravity goes into the velocity function as -32t; in the position function, the antiderivative of velocity, it goes in as -16t^2. The position function is s(t) = -16t^2 + 48t + 400. When you solve that for t, what you get is the time the rock hits the ground. When you find that t value, sub it into the velocity equation to find the velocity at that time the rock hits the ground. Solving for t (using the quadratic equation) you get a t value of 6.720153. The velocity equation, the first derivative, is v(t) = -32t + 48. Subbing the t value of 6.720153 in you get that the velocity is -167.045. Negative is correct here as well because it was positive going up and now it's coming down.

Answer 2

Velocity with which rock will hit the ground is 167.045 feet.

Explanation:

A rock is thrown upward with a speed of 48 feet per second from the edge of a cliff.

So we will calculate the height attained by the rock will be

v² = u² - 2gh [Third equation of vertical motion]

Where v is the final velocity at height and u s the initial velocity f the rock.

For maximum height attained by rock v = 0

0 = 4² - 2 gh

4² = 2 gh

(48)² = 2 × 32 × h

h =
`(48* 48)/(64)=36 feet`

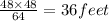
Now rock is at h = height of cliff from the ground + height attained by rocked when thrown upwards.

height h' = 400 + 36 = 436 feet.

By the formula v² = 4² + 2 gh [ third equation of vertical motion ]

here 4 = 0 and h' = 436 feet.

So v² =
`0+2* (3.2)(436)`

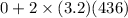
= 27904

v =
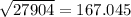`√(27904) = 167.045` feet per second.

Therefore, velocity with which rock will hit the ground is 167.045 feet.