Question

10 points for correct answer!!!!!

Which statements are true about additional information for proving that the triangles are congruent? Check all that apply.
If A ≅ T, then the triangles would be congruent by ASA.
If B ≅ P, then the triangles would be congruent by AAS.
If all the angles are acute, then the triangles would be congruent.
If C and Q are right angles, then triangles would be congruent.
If BC ≅ PQ, then the triangles would be congruent by ASA.

Answer 1

ASA is equivalent
AAS cannot be applied
Acute angles cannot be applied
For right angles, congruent can be proved by SA

Answer 2

ASA(Angle-Side-Angle) theorem states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then that triangles are congruent.

AAS (Angle-Angle-Side)theorems states that if two angles and any side of one triangle are congruent to two angles and any side of another triangle, then the triangles are congruent.

In ΔABC and ΔPQT

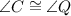`\angle C \cong \angle Q` {Angle] [Given]

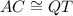`AC \cong QT` [Side] [Given]

(A)

if
`\angle A \cong \angle T` [Angle]

Then, by ASA theorem;

the given triangles are congruent.

(B)

If
`\angle B \cong \angle P` [Angle]

then, by AAS theorem;

the triangles are congruent.

(C)

If all the angles are acute, then the given triangles may not be congruent

(D)

If C and Q are right angles, then the triangles would not be congruent by HL because the leg of hypotenuse are not equal.

(E)

if
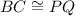`BC \cong PQ` [side]

Then, the given triangle would be congruent only by SAS not by ASA.

Therefore, the Only option A and B are correct.