Question

An epidemic has hit Minecole City. Its population is declining 34% every hour. In just 3 hours, there are only 25,143 people left in the city. What was the initial population in the city before the epidemic broke out?

A) 69,727
B) 69,726
C) 16,595
D) 49,785

Answer 1

yo da answer be D
49,7985

Answer 2

B) 69,726

Explanation:

We have been given that an epidemic has hit Minecole City. Its population is declining 34% every hour.

As population of the city declining 34% per hour, this means that population is decreasing exponentially.

Since we know that an exponential function for continuous growth is in form:
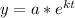`y=a*e^(kt)`, where,

`a=\text{Initial value}`,

`e=\text{Mathematical constant}`,

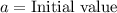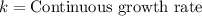`k=\text{Continuous growth rate}` If k>0 then amount is increasing, if k<0 then amount is decreasing.

Let us convert our given rate in decimal form.

`34\%=(34)/(100)=0.34`

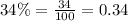
Upon substituting k=-0.34 in exponential decay function we will get,

`y=a*e^(-0.34t)`

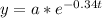
Therefore, the function
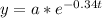`y=a*e^(-0.34t)` represents the population of city after t hours.

As we have been given that in 3 hours there are only 25,143 people left in the city, so to find our initial value we will substitute y=25143 and t=3 in our function.

`25143=a*e^(-0.34*3)`

`25143=a*e^(-1.02)`

`25143=a*0.3605949401730783`

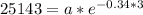
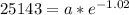
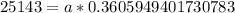
Let us divide both sides of our equation by 0.3605949401730783.

`(25143)/(0.3605949401730783)=(a*0.3605949401730783)/(0.3605949401730783)`

`69726.43595=a`

`a\approx 69726`

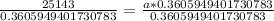
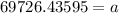
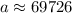
Therefore, the initial population in the city before the epidemic broke out was 69726 and option B is the correct choice.