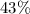Answer: D. 43 %
Explanation:
Let M is the event of receiving medicine,
M' is the event of not receiving medicine,
C is the event of clear skin.
Then According to the question,
Total size of the sample space, n(S) = 100
Number of patient who get the medicine, n(M) = 40
Number of patient who do not get the medicine, n(M') = 60
Number of patient who received the medication reported clearer skin at the end of the study,

Therefore, the probability that patient who received the medication reported clearer skin at the end of the study,
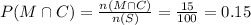
Number of patient who who did not receive the medication reported clearer skin at the end of the study, n(M\capC) = 20.
Thus, the Number of patient who cleared the skin, n(C) = 15 + 20 = 35
And, the probability that the patient cleared their skin,
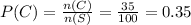
Therefore, the probability that a patient chosen at random from this study took the medication, given that they reported clearer skin,
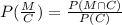
⇒

⇒

⇒
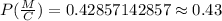
Thus,
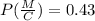 or
or