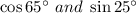Answer: It will be
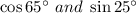
Explanation:
Since we have given that
cos 107° cos 42° + sin 107° sin 42°
As we know the formula :

So, applying the above formula , we get
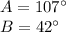
Now, we have to write it in cosine terms,
So, we get,
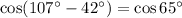
So, in terms of cosine , it will be
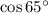
In terms of sine , it will be
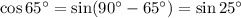
Hence, it will be