Question

Joey is saving up for a down payment on a car. He plans to invest $2,000 at the end of every year for 3 years. If the interest rate on the account is 2.05% compounding annually, what is the present value of the investment? $4,180.20 $5,762.15 $5,891.08 $5,978.76

Answer 1

A=Annual amount=2000
i=annual interest=0.0205
n=number of years=3
Present value
=A((1+i)^n-1)/(i(1+i)^n)
=2000(1.0205^3-1)/(.0205(1.0205^3))
=5762.15

Answer 2

B. $5762.15.

Explanation:

We have been given that Joey plans to invest $2,000 at the end of every year for 3 years. The interest rate on the account is 2.05% compounding annually.

We will use present value formula to solve our given problem.

`\text{Present value}=P*[(1-(1+r)^(-n))/(r)]`, where,

`P=\text{Periodic payment}`,

`r=\text{Rate per period in decimal form}`,

`n=\text{Number of periods}`.

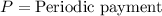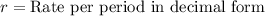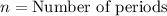Let us convert our given rate in decimal form.

`2.05\%=(2.05)/(100)=0.0205`

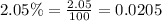
Upon substituting our given values in above formula we will get,

`\text{Present value}=2000*[(1-(1+0.0205)^(-3))/(0.0205)]`

`\text{Present value}=2000*[(1-(1.0205)^(-3))/(0.0205)]`

`\text{Present value}=2000*[(1-0.94093792)/(0.0205)]`

`\text{Present value}=2000*[(0.05906208)/(0.0205)]`

`\text{Present value}=2000*2.88107688`

`\text{Present value}=5762.15376\approx 5762.15`

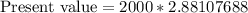
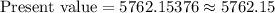
Therefore, the present value of the investment will be $5762.15 and option B is the correct choice.