Question

The ratio of the surface areas of two similar solids is 25:121. What is the ratio of their corresponding side lengths? A. 5:11 B.1 :96 C. 11/25:11 D. 5:121/5

Answer 1

5:11 ~~~~~~~~~~~~~~~~ APEX

Answer 2

A.5:11

Explanation:

We are given that ratio of areas of two similar solids is 25: 121.

We have to find the ratio of their side lengths.

We know that surface area of cube=
`6a^2`

Let x and y be the side of small and large solid

Then,
`(Surface\;area\;of\;small\;solid)/(surface\;area\;of\;large\;solid)=(6x^2)/(6y^2)=(25)/(121)`

`(x^2)/(y^2)=(5^2)/(11^2)`

`((x)/(y))^2=((5)/(11))^2`

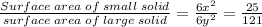
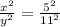
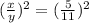
Cancel both side square then, we get

`(x)/(y)=(5)/(11)`

Hence, the ratio of their side length is 5:11.

Answer:A. 5:11