Question

Prove that dx/x^4 +4=π/8

Answer 1

`\displaystyle\int_0^\infty(\mathrm dx)/(x^4+4)`

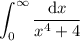
Consider the complex-valued function


`f(z)=\frac1{z^4+4}`

which has simple poles at each of the fourth roots of -4. If
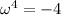
`\omega^4=-4`, then


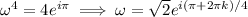
`\omega^4=4e^(i\pi)\implies\omega=\sqrt2e^(i(\pi+2\pi k)/4)` where
`k=0,1,2,3`

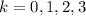
Now consider a semicircular contour centered at the origin with radius
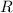
`R`, where the diameter is affixed to the real axis. Let
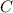
`C` denote the perimeter of the contour, with
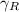
`\gamma_R` denoting the semicircular part of the contour and
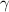
`\gamma` denoting the part of the contour that lies in the real axis.


`\displaystyle\int_Cf(z)\,\mathrm dz=\left\{\int_(\gamma_R)+\int_\gamma\right\}f(z)\,\mathrm dz`

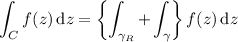
and we'll be considering what happens as
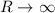
`R\to\infty`. Clearly, the latter integral will be correspond exactly to the integral of
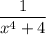
`\frac1{x^4+4}` over the entire real line. Meanwhile, taking
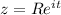
`z=Re^(it)`, we have


`\displaystyle\left|\int_(\gamma_R)(\mathrm dz)/(z^4+4)\right|=\left|\int_0^(2\pi)(iRe^(it))/(R^4e^(4it)+4)\,\mathrm dt\right|\le(2\pi R)/(R^4+4)`

and as
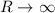
`R\to\infty`, we see that the above integral must approach 0.

Now, by the residue theorem, the value of the contour integral over the entirety of
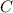
`C` is given by
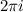
`2\pi i` times the sum of the residues at the poles within the region; in this case, there are only two simple poles to consider when
`k=0,1`.


`\mathrm{Res}\left(f(z),\sqrt2e^(i\pi/4)\right)=\displaystyle\lim_(z\to\sqrt2e^(i\pi/4))f(z)(z-\sqrt2e^(i\pi/4))=-\frac1{16}(1+i)`

`\mathrm{Res}\left(f(z),\sqrt2e^(i3\pi/4)\right)=\displaystyle\lim_(z\to\sqrt2e^(i3\pi/4))f(z)(z-\sqrt2e^(i3\pi/4))=\frac1{16}(1-i)`

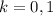
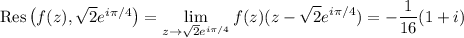
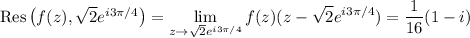
So we have


`\displaystyle\int_Cf(z)\,\mathrm dz=\int_(\gamma_R)f(z)\,\mathrm dz+\int_\gamma f(z)\,\mathrm dz`

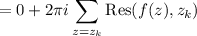
`\displaystyle=0+2\pi i\sum_(z=z_k)\mathrm{Res}(f(z),z_k)` (where
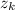
`z_k` are the poles surrounded by
`C`)

`=2\pi i\left(-\frac1{16}(1+i)+\frac1{16}(1-i)\right)`

`=\frac\pi4`

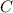
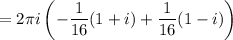
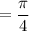
Presumably, we wanted to show that


`\displaystyle\int_0^\infty(\mathrm dx)/(x^4+4)=\frac\pi8`

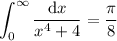
This integrand is even, so


`\displaystyle\int_0^\infty(\mathrm dx)/(x^4+4)=\frac12\int_(-\infty)^\infty(\mathrm dx)/(x^4+4)=\frac12\frac\pi4=\frac\pi8`

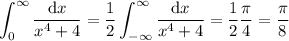
as required.