Question

The surface areas of two similar solids are 450mm squared and 578mm squared. If the volume of the smaller solid is 511mm cubed find the volume of the larger solid. Round your answer to the nearest hundredth.

Answer 1

The volume of the larger solid is 743.86 cubic mm.

Explanation:

The surface areas of two similar solids are 450 mm squared and 578 mm squared.

Since the solids are similar, the ratio of the surface areas is equal to the square of the scale factor, k.

`k^(2)= (578)/(450)` =
`(289)/(225)`

`k=\sqrt{(289)/(225)}`

`k=(17)/(15)`

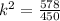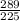
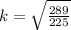
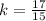
The ratio of the volumes of the solids is equal to
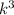`k^(3)`, so further we can solve as:

`(V)/(511) =((17)/(15))^(3)`

`(V)/(511) =(4913)/(3375)`

`V =(4913*511)/(3375)`

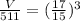
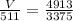
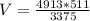
V=743.86 cubic mm.

Answer 2

`\bf \qquad \qquad \textit{ratio relations} \\\\ \begin{array}{ccccllll} &Sides&Area&Volume\\ &-----&-----&-----\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}&\cfrac{s}{s}&\cfrac{s^2}{s^2}&\cfrac{s^3}{s^3} \end{array} \\\\ -----------------------------\\\\ \cfrac{\textit{similar shape}}{\textit{similar shape}}\qquad \cfrac{s}{s}=\cfrac{√(s^2)}{√(s^2)}=\cfrac{\sqrt[3]{s^3}}{\sqrt[3]{s^3}}\\\\ -------------------------------\\\\`


`\bf \cfrac{√(s^2)}{√(s^2)}=\cfrac{\sqrt[3]{s^3}}{\sqrt[3]{s^3}}\implies \cfrac{√(450)}{√(578)}=\cfrac{\sqrt[3]{511}}{\sqrt[3]{v}}\implies \cfrac{15√(2)}{17√(2)}=\cfrac{\sqrt[3]{511}}{\sqrt[3]{v}} \\\\\\ \cfrac{15}{17}=\cfrac{\sqrt[3]{511}}{\sqrt[3]{v}}\implies \sqrt[3]{v}=\cfrac{17\sqrt[3]{511}}{15}\implies v=\left( \cfrac{17\sqrt[3]{511}}{15} \right)^3 \\\\\\ v=\cfrac{17^3\cdot 511}{15^3}`