Question

The longer base of an isosceles trapezoid measures 22 ft. The nonparallel sides measure 8 ft, and the base angles measure 75°. Find the length of a diagonal.

Answer 1

check the picture below

and recall that


`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad cos(\theta)=\cfrac{adjacent}{hypotenuse}\\\\ -------------------------------\\\\ sin(75^o)=\cfrac{y}{8}\implies 8sin(75^o)=y \\\\\\ cos(75^o)=\cfrac{x}{8}\implies 8cos(75^o)=x`

Answer 2

The length of a diagonal is 21.44 feet ( approximately).

Explanation:

Given a trapezoid ABCD

AD= 22 feet

DC=8 feet

AD= DE+EA

Let DE=x and CE= y

In triangle DEC

`(DE)/(DC)=cos75^(\circ)`

`(x)/(8)=0.2588`

`x= 0.2588*8`

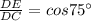
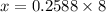
x= 2.070

DE=x=2.0 feet( approximately)

`(CE)/(DC)=sin75^(\circ)`

`(y)/(8)=0.9659`

`y=8*0.9659`

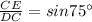
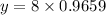
y=7.7274

y=7.73( approximately)

CE=7.73 feet

EA= AD-DE=22-2=20 feet

In triangle AEC

Usin pythogorous theorem

`(CE)^2+(EA)^2=(AC)^2`

`(7.73)^2+(20)^2=(AC)^2`

`(AC)^2= 59.7529+400`

`AC=√(459.7529)`

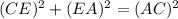
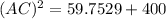
AC=21.44 feet (approximately)

Hence, the length of diagonal =21.44 feet ( approximately).