Question

Find real points satisfying 3x^2+3y^2-4xy+10x-10y+10=0

Answer 1

Given

`3x^2+3y^2-4xy+10x-10y+10=0`
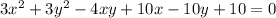
This can be rewritten as follows:

`3y^2+(-4x-10)y+(10+10x+3x^2)=0`

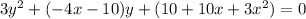
Notice that this is a quadratic equation of the form:

`ay^2+by+c=0`,
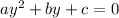
with the solution given by:

`y= (-b\pm √(b^2-4ac) )/(2a)`
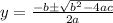
where:

`a = 3, \\ b = -4x - 10 \\ c = 10 + 10x + 3x^2`

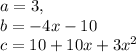
Thus,

`y= (-(-4x-10)\pm √((-4x-10)^2-4(3)(10+10x+3x^2)) )/(2(3)) \\ \\ =(4x+10\pm √((16x^2+80x+100)-12(10+10x+3x^2)) )/(6) \\ \\ =(4x+10\pm √(16x^2+80x+100-120-120x-36x^2) )/(6) \\ \\ =(4x+10\pm √(-20x^2-40x-20) )/(6) \\ \\ =(4x+10\pm 2√(-5x^2-10x-5) )/(6)`

Now consider

`√(-5x^2-10x-5)`
This gives a real solution if and only if

`-5x^2-10x-5 \geq 0`
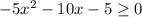
i.e.

`-5(x^2+2x+1) =0 \\ \\ (x+1)^2=0 \\ \\ x+1=0 \\ \\ x=-1`

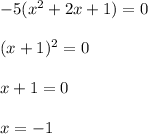
Thus,

`-5x^2-10x-5 \geq 0`
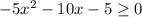
when x = -1

Thus, the equation has real solutions only when x = -1 at which the value of y is given by

`y=(4(-1)+10\pm 2√(-5(-1)^2-10(-1)-5) )/(6) \\ \\ =(-4+10\pm 2√(-5+10-5) )/(6) =(6\pm 2√(0) )/(6) =(6\pm 2(0) )/(6) \\ \\ =(6\pm 0 )/(6) = (6)/(6) =1`

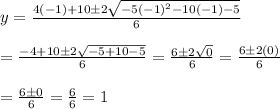
Therefore, the real point satisfying

`3x^2+3y^2-4xy+10x-10y+10=0`
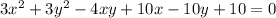
is x = -1, y = 1