 simplifies to
simplifies to
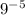 , representing the reciprocal of
, representing the reciprocal of
 . This follows the rule
. This follows the rule
 , showcasing the exponent subtraction when dividing powers of the same base.
, showcasing the exponent subtraction when dividing powers of the same base.
To simplify
 , apply the rule
, apply the rule
 for the same base a. In this case, both bases are 9.
for the same base a. In this case, both bases are 9.
![\[(9^2)/(9^7) = 9^(2-7) = 9^(-5)\]](https://img.qammunity.org/2018/formulas/mathematics/middle-school/m4446uezx2czm2z4t3f38hyogzszv17its.png)
So,
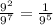 or
or
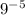 .
.
The expression
 simplifies to
simplifies to
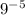 using the rule
using the rule
 . This simplification represents the reciprocal of
. This simplification represents the reciprocal of
 , emphasizing the inverse relationship between the numerator and denominator.
, emphasizing the inverse relationship between the numerator and denominator.
Thus, the result is a fraction with the base 9 raised to the power of -5, indicating that the expression is equivalent to
 . This showcases the mathematical principle of exponent subtraction when dividing powers of the same base, resulting in a concise and simplified form for the given expression.
. This showcases the mathematical principle of exponent subtraction when dividing powers of the same base, resulting in a concise and simplified form for the given expression.