1. let Carmen's average speed (her rate) be r when she goes from her house to the market
Carmen's rate when she comes back is 3/4r
2. let t be the time it takes Carmen to go from her house to the market
The same distance d, from house to market can be described with:
(i)
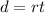
(as she goes to the market)
and (ii)
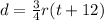
(as she comes back to her house)
so
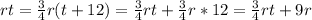
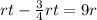
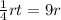
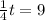
t=36 (min), so t+12=48 min
answer: 48 min