ANSWER:
The best method is : is elimination by substitution
Step-by-step explanation:
First we must eliminate one of the variables in both equations, that is, x, to find y, then we must substitute the value of y in one of the equations to find the value of x
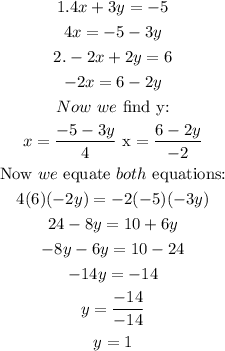
Now we must replace that value in both equations to have the value of x.
(The value of x must be the same for the two equations ;If the value of x is the same that means that the value of y was correctly found.,)
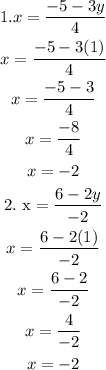
To verify that the system is well solved, those values found must be replaced in the original equation and it must give us the value of the equation.
1.EQUATION:
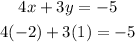
We can see by replacing the values found for x and for y that it gives us -5 which shows that the system was correctly developed.
2.EQUATION:
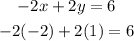
Again we replace the found values of x and y in the second equation and it gives us the answer correctly, which confirms that the system was perfectly developed.