Question

Let f(x)=e^x and g(x)=x-3 what are the domain and range of (f g) (x)

A. domain: x>0 range: y<0
B. domain: x>3 range y>0
C. domain: al real numbers range: y<0
D. domain: all real numbers range: y>0

Answer 1

(f of g)(x)=f(g(x))=f(x-3)=e^(x-3)
The domain of a real exponential function is all real, and
the corresponding range is y>0, i.e. (0,+&infin;)

Answer 2

D. domain: all real numbers range: y>0

Explanation:

The composite function of f(x) and g(x) is:

y = f(g(x))

In this problem, we have that:

`f(x) = e^(x)`

`g(x) = x - 3`

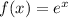
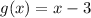
So

`f(g(x)) = f(x - 3) = e^(x - 3)`

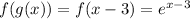
The domain of an exponential function is all real numbers, and the range are positive values.

So the correct answer is:

D. domain: all real numbers range: y>0