Question

Use a sum or difference formula to find the exact value of the following.cos

Answer 1

The identity of the sum of cos two angles is

`\text{cos(a}+b)=\cos a\cos b-\sin a\sin b`

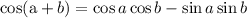
Since the given expression is

`\cos (3\pi)/(7)\cos (9\pi)/(28)-\sin (3\pi)/(7)\sin (9\pi)/(28)`

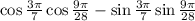
Compare it with the identity above

`\begin{gathered} a=(3\pi)/(7) \\ b=(9\pi)/(28) \end{gathered}`

Then the expression can be written as cos (a + b)

`\cos (3\pi)/(7)\cos (9\pi)/(28)-\sin (3\pi)/(7)\sin (9\pi)/(28)=\cos ((3\pi)/(7)+(9\pi)/(28))`

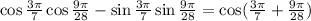
To add the 2 angles equalize their denominators by finding LCM of them

Since LCM of 7 and 28 is 28, then

`\cos ((3\pi)/(7)+(9\pi)/(28))=\cos ((12\pi)/(28)+(9\pi)/(28))=\cos ((12\pi+9\pi)/(28))=\cos ((21\pi)/(28))`

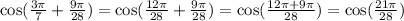
Now we need to find cos (21pi/28)

Since the angle of measures 21pi/28 = 3pi/4 in its simplest form

Since the angle 3pi/4 is greater than pi/2 and pi, then it lies in the second quadrant

The measure of any angle in the second quadrant is between pi/2 and pi, and the value of cos any angle in the second quadrant is negative

`\begin{gathered} \cos ((3\pi)/(4))=-\cos (\pi)/(4) \\ \cos (\pi)/(4)=\frac{\sqrt[]{2}}{2} \\ \cos (3\pi)/(4)=-\frac{\sqrt[]{2}}{2} \end{gathered}`

The answer is

`-\frac{\sqrt[]{2}}{2}OR-\frac{1}{\sqrt[]{2}}`