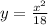Question

The graph shows the distance, in feet, required for a car to come to a full stop if the brake is fully applied and the car was initially traveling x miles per hour.

Which equation can be used to determine the stopping distance in feet, y, for a car that is traveling x miles per hour?

y = (1/18)^x
y = (1/5)^x
y = x^2/18
y = x^2/5

Answer 1

y=
`(x^(2) )/(18)`

Answer 2

The correct equation should model the data shown in the figure.
We shall test two values: (30,60) and (60, 200).

Test y = (1/18)^x
x=30 => y = (1/18)^30 = 0 Incorrect

Test y = (1/5)^x
x = 30 => y = (1/5)^30 = 0 Incorrect

Test y = x^2/18
x = 30 => y = 30^2/18 = 50 Correct
x = 60 => y = 60^2/18 = 200 Correct

Test y = x^2/5
x = 30 => y = 30^2/5 = 180 Incorrect

Answer:
The correct equation is
`y= ( x^(2) )/(18)`