Final answer:
The frame cannot be rectangular because the measured diagonal length across the frame does not match the expected length based on the given dimensions.
Step-by-step explanation:
The completed frame cannot actually be rectangular because the measured diagonal length across the frame does not match the expected length based on the given dimensions of the length and width. In a rectangular frame, the length, width, and diagonal form a right triangle.
Using the Pythagorean Theorem, we can determine the expected diagonal length of a rectangular frame with length = 14 inches and width = 10 inches:
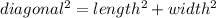
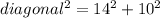
= 196 + 100
= 296
= √296
diagonal ≈ 17.17 inches
Since the measured diagonal length is 20 inches, which is larger than the expected diagonal length, the frame cannot be a rectangle.