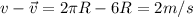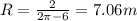Question

a particle is moving in a circle of radius R with constant speed.The time period of particle is T=1 second.In a time t=T/6,if the difference between average speed and magnitude of average velocity of particle is 2 m/sec,find the radius of circle

Answer 1

at t=T/6, total distance covered= 2*pi*r/6 and displacement= r

difference of them = 2*t
so, 2*pi*r/6- r =2(1/6)=1/3

r=1/(pi-3)=7.062

Answer 2

R = 7.06 m

Step-by-step explanation:

As we know that time period of the particle is T = 1 s

so the angle covered by it in t = T/6 seconds is given as

`\theta = (2\pi)/(T)t`

`\theta = (2\pi)/(1)* (1)/(6)`

`\theta = (\pi)/(3)`

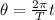
now we know that total distance moved by the particle will be

`d = R\theta = R* (\pi)/(3)`

now average speed is given as

`v = (R* (\pi)/(3))/((1)/(6))`

`v = 2\pi R`

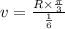
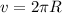
now for displacement of the particle we know that

`\vec d = \sqrt{R^2 + R^2 - 2(R)(R)cos(\pi)/(3)}`

`\vec d = R`

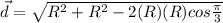
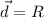
so average velocity is given as

`\vec v = (R)/((1)/(6)) = 6R`

now we have

`v - \vec v = 2\pi R - 6 R = 2 m/s`

`R = (2)/(2\pi - 6) = 7.06 m`