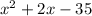Question

How can you determine if a function is a quadratic function from its equation?

Answer 1

A quadratic function is a polynomial of degree 2.
Therefore if a function is a quadratic function, it should have the term
`x^(2)` in its expression.

A quadratic function has the form

`f(x) = a x^(2) + bx + c`
where
`a, b`, and
`c` are constants.

Although
`b` and/or
`c` can be zero,
`a` should not be zero.

Answer 2

Any quadratic equation always comes in the form

`a x^(2) +bx+c=0`

where a, b, and c are constant.

few examples;

`x^(2) +3x+4=0`
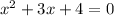
where
`a=1`,
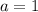
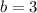
`b=3`, and
`c=4`


`-4 x^(2) -9x+5=0`
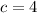
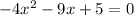
where
`a=-4`,
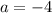
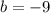
`b=-9`, and
`c=5`


`35 x^(2) -56x=198`
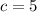
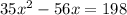
At first, this equation doesn't look like a quadratic equation but with a little rearranging, it will.

`35x^(2)-56x-198=0`


`(x-5)(x+7)`
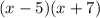
This form also needs to be manipulated to get the quadratic form; by multiplying out we have
`x^(2) +2x-35`