Hello there. To solve this question, we'll have to remember some properties about scaling factor and ratios.
Given two solids that are similar:
We have to determine the scaling factor, the surface area and volume ratios.
First, the scaling factor, in the case of spheres, is the ratio between their radius.
In this case, we determine each ratio using the formula for the volume:
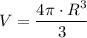
For a sphere with radius R.
In our case, say the smaller sphere has radius r and the larger sphere has radius R.
Hence we have that:
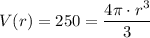
Multiply both sides of the equation by a factor of 3/4pi
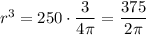
Take the cube root on both sides of the equation
![r=\sqrt[3]{(375)/(2\pi)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/164tr2ijygqszd081i0i.png)
We're not using an approximation here because we'll need this value until the end.
Now, for the sphere with radius R, we have
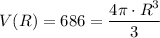
Multiply both sides by 3/4pi
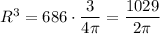
Take the cube root on both sides of the equation
![R=\sqrt[3]{(1029)/(2\pi)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/bc5a42fbwfjjygx44smx.png)
The scaling factor is given by:
![(R)/(r)=\frac{\sqrt[3]{(1029)/(2\pi)}}{\sqrt[3]{(375)/(2\pi)}}=\sqrt[3]{(343)/(125)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/c4scpdb3tl7virtq0cut.png)
Now, we can find an approximation for it as:
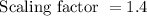
In fact it is exact.
Now, to find the surface area and volume ratios, we use the formulas to show that:
The surface area of a sphere with radius R is
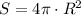
Hence the ratio is

Plugging the solution we found, we get
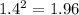
In a same manner for a volume, we get
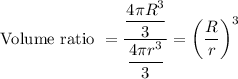
Hence we get
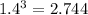
These are the answers to this question.