Question

The wildlife department has been feeding a special food to rainbow trout fingerlings in a pond. based on a large number of observations, the distribution of trout weights is normally distributed with a mean of 402.7 grams and a standard deviation 8.8 grams. what is the probability that the mean weight for a sample of 40 trout exceeds 405.5 grams?

Answer 1

The normal distribution curve for the problem is shown below

We need to standardise the value X=405.5 by using the formula


`z-score= (X-Mean)/(Standard Deviation)`

`z-score= (405.5-402.7)/(8.8) =0.32`

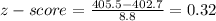
We now need to find the probability of z=0.32 by reading the z-table

Note that z-table would give the reading to the left of z-score, so if your aim is to work out the area to the right of a z-score, then you'd need to do:


`P(Z\ \textgreater \ z)=1 - P(Z\ \textless \ z)`

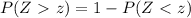
from the z-table, the reading
`P(Z\ \textless \ 0.32)` gives 0.6255

hence,

`P(Z\ \textgreater \ 0.32)=1-0.6255=0.3475`

The probability that the mean weight for a sample of 40 trout exceeds 405.5 gram is 0.3475 = 34.75%